
The new descriptions of strength, linearity and direction. Given a new set of scatterplots below, repeat the same exercise, but now with Portland, OR) there is a strong, linear trend. Though there are a few outliers (citiesĪlong the northwest coast of the US that have temperate winters, such as Negative direction, as the greater the latitude, the colder the The two functions that can be used to visualize a linear fit are regplot () and lmplot ().
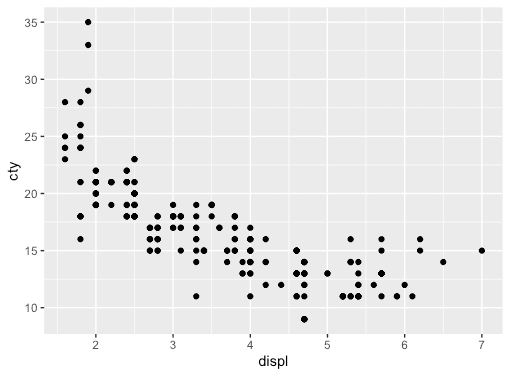
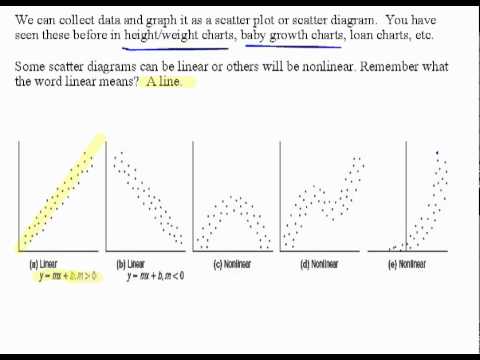
Scatter plots are described as linear orįor example, the scatterplot of latitude and January temperatures had The linearity of scatter plot indicates how close the points are If the points are clearly clustered, or closelyįollow a curve or line, the relationship is described as strong. Computation of a basic linear trend line is also a fairly. The more spread out the points are, the weaker The scatter plot is a basic chart type that should be creatable by any visualization tool or solution. The strength of a scatter plot is usually described as weak, Increases, or the points of the scatterplot go down from left to We say this is bivariate data and we plot the data from two different sets using. The explained variable decreases as the explanatory variable A scatter-plot is a graph that shows the relationship between two variables. Increases as the explanatory variable increases, or the points of the The linear relationship is strong if the points are close to a straight line, except in the case of a horizontal line where there is no relationship. The direction is positive when the explained variable In this chapter, we are interested in scatter plots that show a linear pattern. The direction of a scatter plot can be described as positive or When describing the shape of the scatter plot and the relationshipīetween the explanatory and explained variable, there are three important This exercise would be simpler given uniform adjectives that everyone could
LINEAR SCATTER PLOT DRIVERS
Similarly, drivers with less driving experience are considered riskier and pay greater premiums. If there is, as in our first example above, no apparent relationship. And if y tends to decrease as x increases, x and y are said to have a negative correlation. If y tends to increase as x increases, x and y are said to have a positive correlation. Ĭorrect: Drivers with more driving experience are considered safer, so they pay smaller premiums. A scatter plot is used to determine whether there is a relationship or not between paired data.Step 2: Method 1: Use Hypothesis test method with a given. (y) is the insurance premium paid for a sample of drivers. To determine if matched pair (x, y) has linear correlation: Step 1: Check scatter plot, If non -linear pattern exists, conclude no linear correlation. Plt.Q-6: The explanatory variable (x) is the years of driving experience and the explained variable Then just draw the two plots: import matplotlib.pyplot as plt If x_data and y_data are numpy arrays: x_mean, y_mean = np.mean(x_data), np.mean(y_data)īeta = np.sum((x_data - x_mean) * (y_data - y_mean)) / np.sum((x_data - x_mean)**2) The scatter diagram graphs pairs of numerical data, with one variable on each axis, to look for a relationship between them. X_var = sum((xi - x_mean)**2 for xi in x_data)
Click the Insert tab, and then click Insert Scatter (X, Y) or Bubble Chart. If x_data and y_data are lists: x_mean = sum(x_data) / len(x_data)Ĭovar = sum((xi - x_mean) * (yi - y_mean) for xi, yi in zip(x_data, y_data)) Select the data you want to plot in the scatter chart. Simple regression coefficients have a closed form solution so you can also solve explicitly for them and plot the regression line along with the scatter plot. The visual pattern in a graph or plot can often reveal the nature of the relationship between two variables. Sns.regplot(x=x_data, y=y_data, ci=False, line_kws=, ax=axs) You can even draw the confidence intervals (with ci= I turned it off in the plot below). The difference is that with a scatter plot, the decision is. The seaborn library has a function ( regplot) that does it in one function call. The regression equations for the two trend lines are given in the lower right of graph relative to the rescaled data, with the linear equation in black and the. Scatter plots are similar to line graphs in that they start with mapping quantitative data points. Trendline for a scatter plot is the simple regression line.


 0 kommentar(er)
0 kommentar(er)
